Press 'o' to toggle the slide overview and 'f' for full-screen mode.

Choose the theme in which to view this presentation:

Black - White - League - Sky - Beige - Simple
Serif - Blood - Night - Moon - Solarized



Copyright © John Lindsay, 2015

Remember, this is where the content for the final exam begins

Raster querying: Reclassification

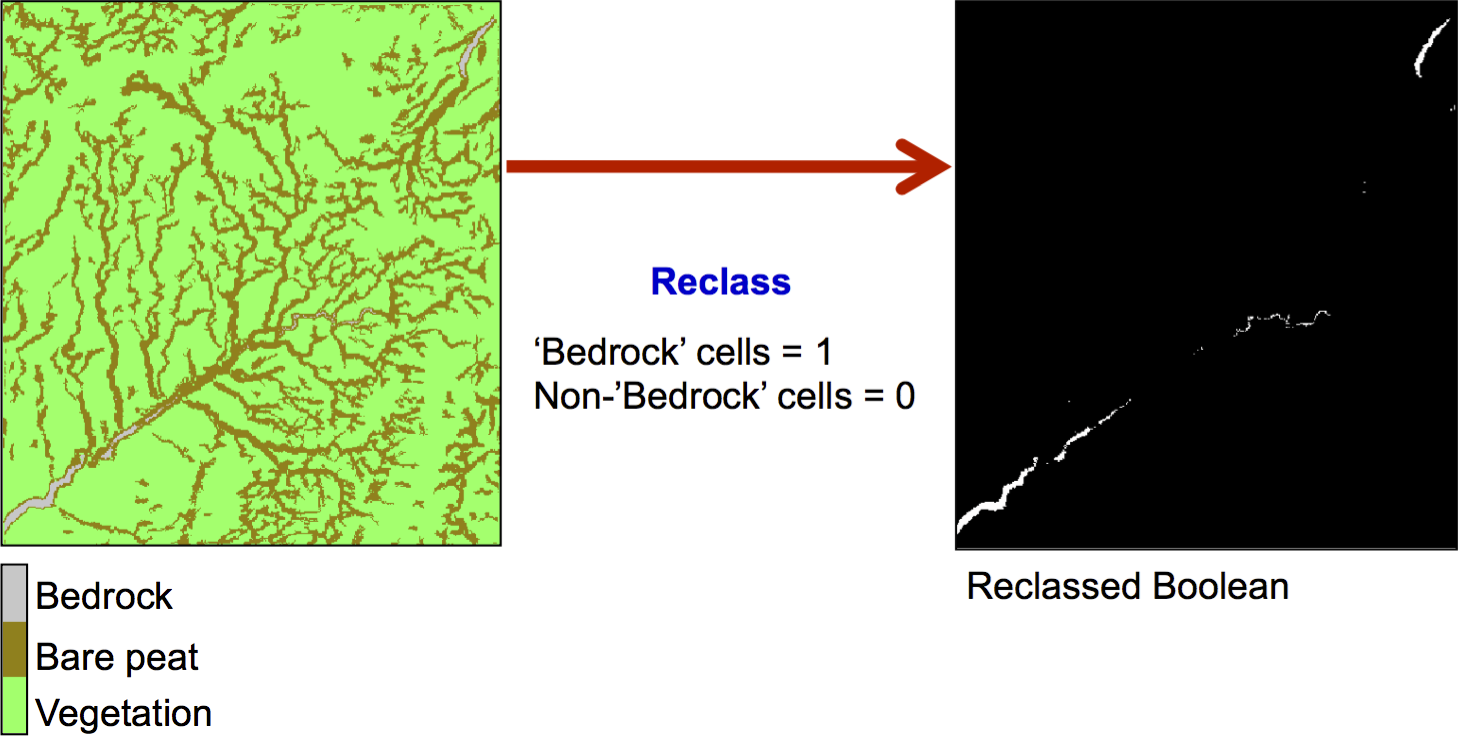
Raster querying: Reclassification

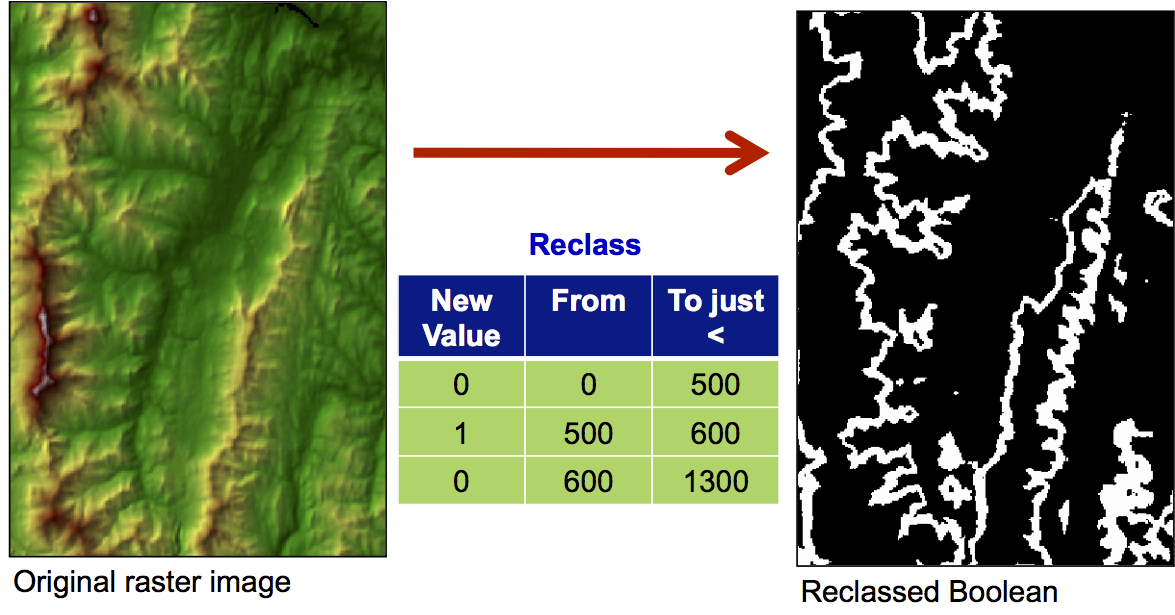
Raster querying: Reclassification

• It is possible to build complex queries involving combinations of query questions in the raster data model by using reclass, map algebra and/or Boolean logical operations, and other spatial analysis operations (e.g. distance, buffering, and area calculations).


• It is possible to perform any spatial query using either the raster or vector data model, but it generally involves more steps using the raster approach

Raster Buffering

• In a raster model, buffer creation is a two-step procedure:
  1. The distance from each cell to the target cell(s) is calculated
  2. Using resulting map is reclassified so that cells with values less than the buffer distance are given the same code

Distance in the Raster Model

• Most modern GIS estimate the Euclidean distance of each raster grid cell to the nearest target cell
  • Based on the highly efficient, 4-pass distance transform of Shih and Wu (2003)


• Some do not and some offer alternatives based on spread functions which iteratively calculate distance through grid cells.

Distance in the Raster Model

• Why use spread to calculate distance?
  • Until Shih and Wu (2003) spread has been far more efficient to estimate than Euclidean distance
  • Spread is a powerful function for performing weighted distance operations, e.g. Least-cost analysis (more to come on this later)


• Spread is less accurate but more powerful

Local Operations: Raster Map Overlay

• How are discrete spatial entities represented in raster?
  • Point is a single cell
  • Line is a cell-wide string of cells
  • Area is a contiguous group of cells


• Raster map overlay works on a cell-by-cell basis
  • Operations are performed on individual cells from two or more input layers to produce a new layer

Raster overlay and map algebra

Comparison Operators

• Equal to, not equal to, greater than, less than, greater than or equal to, less than or equal to (= , <>, >, < , >= , <=)


• > and < operators are like a simple reclassification


• Input images are not necessarily Boolean images but the output image is always a Boolean

Comparison Operators

Comparison Operators

Comparison Operators

The MIN and MAX Operators

• MIN('Map1', 'Map2') & MAX('Map1', 'Map2', 'Map3')


• Assigns each cell in the output image the minimum (or maximum) value for the corresponding cells in the input maps


• You may have two or more input maps

Mathematical operators

• Map addition, subtraction, multiplication, and division


• One-map/one-constant operations vs. two-map ops
  • 'Map1' + 10
  • 'Map1' - 'Map2'


• Why might you want to multiply or divide all the values in an image by a constant (e.g. 'Map1' / 3.281)?

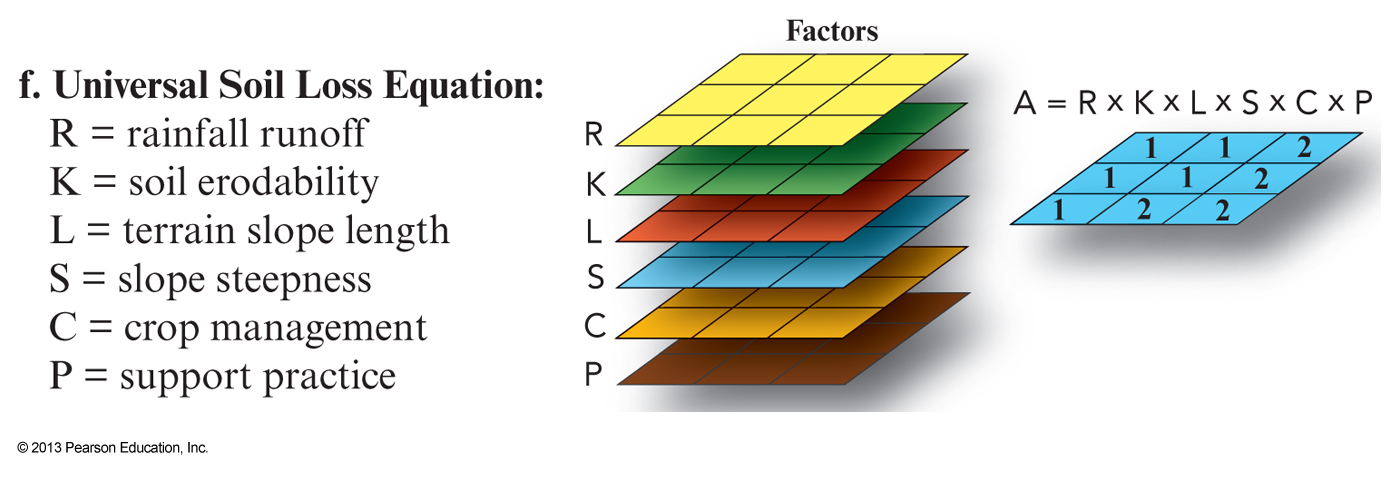
Other map algebra possibilities

• Complex mathematical combinations are possible
  • e.g. Ln['catchmentAreaMap' / tan('slopeMap')]
  • Must be careful not to divide by zero!

Considerations with raster map overlay

• Grid cell resolution...how to cope with incompatible resolutions of input images?
• Scale of input data, i.e. dichotomous (Boolean), nominal (categorical), ordinal, interval, ratio
• Rarely perform a single operation; most GIS analyses require several operations performed in series with several intermediate steps